Funciones 2°

Función Cuadrática Toda función de segundo grado o cuadrática en la variable x puede expresarse por:  f(x)=ax² +bx+c donde a, b y c son números reales, con .Las funciones cuadráticas tienen las siguientes particularidades: Su representación gráfica en el plano real es una parábola. El dominio es el conjunto de los números reales, salvo que se indique lo contrario. La imagen es un subconjunto de los números reales y depende de los valores de a, b y c.

Las características generales de las funciones polinómicas de segundo grado son:

1) El dominio de las funciones cuadráticas es R.

2) Tiene un eje de simetría cuya fórmula es:

     

3) El vértice de la parábola es:

     

4) Corta al eje X en dos puntos, uno o ninguno, según el número de raíces reales de   ax² + bx + c = 0.

5) Corta el eje Y en el punto   (0, c).

6) El vértice es un mínimo si   a > 0   y un máximo si   a < 0.

7) Es cóncava si   a > 0   y convexa si   a < 0.

8) Al aumentar   a   en valor absoluto, la parábola se hace más estrecha.

Tipos de funciones cuadráticas

En una función cuadrática   f(x) = ax² + bx + c,  con   a ≠ 0 .

Si   b = 0   y   c = 0

  

Tipos de funciones cuadráticas

En una función cuadrática   f(x) = ax² + bx + c  ,  con   a ≠ 0 .

Si   b = 0   y   c = 0

La función   f(x) = ax²   tiene su vértice en el punto   (0, 0)   y su eje de simetría es el eje Y.

Si   b = 0   y   c ≠ 0

La función   f(x) = ax² + c   tiene su vértice en el punto   (0, c)   y su eje de simetría es el eje Y.

Si   b ≠ 0   y   c = 0

La función   f(x) = ax² + bx   tiene su vértice y su eje de simetría en:

      

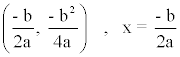
Puedes hacer un ejercicio en:

https://www.geogebra.org/m/tEw3a5yc

Parte corregida 

Una función cuadrática es una función que puede ser descrita por una ecuación de la forma y = ax² + bx + c, donde a ≠ 0. Ningún término en la función polinomial tiene un grado mayor que 2. Las funciones cuadráticas son útiles cuando trabajamos con áreas, y frecuentemente aparecen en problemas de movimiento que implican gravedad o aceleración.

Las gráficas de las funciones cuadráticas tienen características que están estrechamente relacionadas con su forma simbólica. 

Una función cuadrática es un polinomio de grado 2, es decir, el exponente más alto en la variable es 2. Los siguientes son ejemplos de funciones cuadráticas:

                                                  y=-3x²

y=x²-4x+4

y=-2(x+1)²-6

La función cuadrática más básica y simple tiene la ecuación y=x²

. Si hacemos una tabla con los valores de esta función, vemos que el rango (los valores de y, o salida) no se comportan como una función lineal. En una función lineal, el valor de y cambia por la misma cantidad cada vez que el valor de x aumenta por 1. Eso no sucede con una función cuadrática:

x	y = x2
-3	9
-2	4
-1	1
0	0
1	1
2	4
3	9